
https://www.sinotechmachinery.com/products/two-stage-multi-stage-fermenter-10l-100l-automatic-sip/
Commercial production of recombinant therapeutic proteins typically involves the suspension culture of mammalian cells in bioreactors with volumes up to 10,000 L. With advances in cell engineering, basal and fed media development, and bioprocess engineering over the past 30 years, expression titers ~10 g/L, viable cell densities >3 × 10^7 cells/mL, and unit cell productivity > 20 pg/cell/day is now common. Such high cell densities (potentially higher) increase mixing and aeration requirements and may subject cells to a harsh environment subject to high hydrodynamic stresses. Previously in this part of the bioreactor scale-up course series, this installment provides a basic understanding of fluid flow, mixing, and mass transfer in bioreactors, and how the interaction of these parameters creates the environment in which cells exist. This can significantly affect cell growth, metabolism and protein production.
Fluid flow in bioreactor:
Fluids (liquids or gases) are substances that continuously deform when subjected to shear forces. Shear causes deformation, a change in the relative positions of fluid components. This force must be applied to create fluid flow. Scientists classify fluids based on their density and viscosity
• Compressible (or incompressible) - whether their density changes with pressure, gases are generally compressible, liquids are incompressible
• Viscosity (all fluids have a finite viscosity, which is the cause of "internal friction" during flow, or expressed as the fluid's resistance to motion)
• Newtonian or non-Newtonian, depending on whether they obey Newton's law of viscosity.
Shear stress is calculated by dividing the shear force exerted on the fluid by the cross-sectional area where the force is applied. Strictly speaking, shear stress is one of two basic fluid dynamics, the other being "normal stress." Both are usually determined by multiplying the viscosity by the velocity gradient, with the flow direction being vertical for shear stress and parallel for normal stress. Therefore, for shear stress, the velocity gradient is written as dUx/dy and for normal stress, the velocity gradient is written as dUx/dx, where U is the fluid velocity and x and y represent the direction of the force/stress.
When a fluid flows through a pipe or solid object, the velocity of the fluid changes depending on the location. For example, a fluid layer in contact with a pipe wall is assumed to have the same velocity as the wall or solid object (zero velocity). Due to the overall fluid motion, the next fluid layer inward has a slightly higher velocity, the layer further inward has a faster velocity, and so on. In every fluid, particles are constantly exchanged between these layers, which affects how quickly they flow. Particles moving from a slow-moving layer to a faster layer have their speed reduced; particles moving from a fast layer to a slower layer have an acceleration effect. Therefore, fluid flow creates shear stress due to velocity differences.
Depending on the fluid velocity, flow can be classified as laminar or turbulent. When the overall fluid motion is slow, adjacent layers of fluid move in an orderly (more or less parallel) motion, called laminar flow. In fast-flowing fluids, fluid particles and fluid clumps often flow randomly and chaotically across layers in a turbulent flow.
The Reynolds number ( Re ) is a dimensionless variable used to describe whether fluid motion is laminar or turbulent. Equation 1 calculates Re for fluid flow in a circular cross-section pipe:
Re = DUρ/μ, where D is the pipe diameter, U is the fluid velocity, and ρ and μ are the density and viscosity of the fluid, respectively.
Since the biopharmaceutical industry is primarily interested in fluid flow in mechanically stirred fermenter, the relevant Reynolds number is defined by Equation 2:
Rei = Ni Di2ρ/μ, where Ni is the impeller velocity, Di is the impeller diameter, and ρ and μ are the density and viscosity of the fluid, respectively.
Conceptually, the Reynolds number represents the ratio of inertial forces to viscous forces. During laminar flow (low Reynolds numbers), viscous forces dominate and the fluid moves slowly. However, as the Reynolds number increases, inertial forces become more dominant and the flow transitions from laminar to turbulent - and then to fully turbulent at sufficiently high Re values.
If Re < 2100 , the pipe flow is laminar. For Re values of 2000–4000, the flow is considered to be in the transition regime from laminar to turbulent. Once Re > 4000, the flow is fully turbulent. In a stirred tank, the Re value that marks the transition from laminar to turbulent flow depends on the geometry of the tank and the impeller.
Turbulence in Bioreactors:
Turbulence is the flow regime encountered by cells in biotechnology bioreactors. Turbulence is essential for efficient mixing (mass and heat transfer in the fluid), so achieving turbulent conditions in the bioreactor is critical for successful culture. As mentioned above, the Reynolds number represents the time over which turbulence develops. As this number increases, inertial forces begin to dominate the viscous forces in the fluid, overcoming the tendency of viscous effects to suppress flow instabilities. Turbulence can therefore be viewed as a highly disordered fluid motion resulting from the growth of instabilities in an initially laminar flow field.
Turbulence is inherently very complex, and our understanding of it is far from complete. The flow has an overall direction, but on top of this is superimposed secondary chaotic motions of fluid particles, causing flow deviations and generating eddies of varying shapes, sizes, velocities, and directions of rotation. These irregular secondary motions in turbulence have a significant impact on mixing efficiency, energy losses, and shear intensity. Turbulence forms rotating fluid structures called eddies, which can stretch, coalesce, and break apart. The fluid velocity within an eddy undergoes large changes in magnitude and direction over relatively short distances and times.
Eddies of varying sizes occur in turbulent flow. The size of the largest eddies is limited by the boundaries of the flow system. Thus, the diameter of the largest eddies in a bioreactor is similar to (but slightly smaller than) the diameter of the reactor vessel. Large eddies are unstable and give rise to smaller eddies, which in turn give rise to smaller eddies, and so on. In a stirred bioreactor, the energy of the large eddies comes from the bulk flow generated by the impellers, so they contain most of the turbulent kinetic energy. The smallest eddies are unable to maintain rotational motion and lose energy as heat due to the effects of viscosity and fluid friction. Therefore, maintaining turbulence requires a continuous supply of energy to replace the energy lost as heat.
Dispersion is the process of breaking up the bulk flow into smaller and smaller eddies to facilitate rapid transport of material throughout the vessel. The degree of uniformity that can be produced by dispersion is limited by the size of the smallest eddy that forms. Assuming isotropic turbulence in the stirred vessel and that the flow is turbulent (NRei > 104 ), the size of the smallest eddy is roughly equal to the Kolmogorov mixing scale (λ) or turbulence scale, defined by Equation 3:
λ= (ν3/ε)1/4
where λ is the characteristic length of the smallest eddy, ν is the kinematic viscosity of the fluid, and ε is the local turbulent energy dissipation rate per unit mass of the fluid.
In steady state, the average rate of turbulent energy dissipation throughout the bioreactor is equal to the power input to the tank fluid by the impeller. Therefore, the greater the power input to the impeller, the smaller the eddies. Since λ depends on viscosity, for a given power input, smaller eddies are generated in low viscosity media. For an energy input of 0.1 W/kg (currently considered high for animal cell culture), the minimum eddy diameter λ is estimated to be about 0.06 mm (60 μm). This represents the minimum mixing scale achievable by dispersion under these conditions.
The characteristic length (λ) of the smallest eddy is often an indicator of the potential for cell damage due to fluid shear. Experiments have shown that if biological entities (e.g., mammalian cells) in a bioreactor are smaller than λ, shear damage to such entities will not occur. Minow et al. compared mixing and mass transfer in two different 1000 L single-use bioreactors. The authors calculated the Kolmogorov scale for the smallest eddy present in each bioreactor type.
As shown in Table 1, the calculated λ values for each bioreactor type were close to 80 μm - much larger than the 15 μm size of the Chinese hamster ovary (CHO) cells used in this study. Similarly, Godoy-Silva et al. described CHO cells that could withstand ≤6000 W/kg power input. At power dissipation rates >300 W/kg, which is still much higher than the power density of commercial cell culture reactors, the only effect observed was the glycosylation pattern of the expressed protein, but the cells were not affected. Even though these results apply only to the system studied, they still suggest that shear damage has been overestimated in recent decades. Nienow came to the same conclusion in two different papers. Therefore, it is safe to say that eddies smaller than 10–20 μm (smaller than typical mammalian cell size) have very little turbulent kinetic energy, whereas larger eddies merely carry cells in convection.
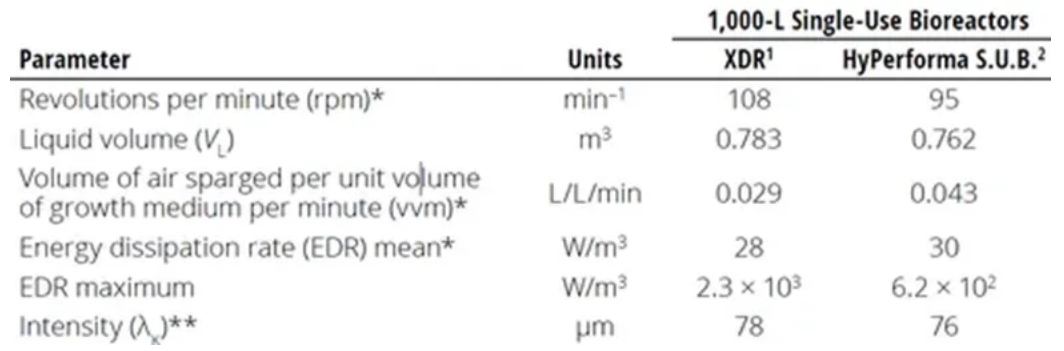
Table 1: Comparison of parameters for calculating fluid dynamic stress in two different 1000L single-use bioreactors. *Maximum values in process at current bioreactor size **Calculated from EDR averages
Mixing is a physical operation that reduces fluid inhomogeneities by eliminating gradients in temperature, concentration, and other properties. During mixing, the exchange of material between different locations in a vessel (e.g., a mixing vessel or bioreactor) results in “mixing” of components. Mixing is widely used in bioprocessing, for example
• Mixing soluble components of powdered culture media with water in preparation for cell culture• Dispersing gases such as air and oxygen through a liquid in the form of bubbles• Maintaining suspension of solid particles such as cells or cell aggregates (e.g., on microcarriers)• Facilitating heat transfer to or from a liquid.
Mixing is one of the most important unit operations in bioprocessing. It is not enough to simply load a bioreactor fermentor with nutrient-rich culture media and cells. Unless the contents of the bioreactor are mixed well, cells will settle and nutrient depletion zones will form as they rapidly consume the substances they need in their local environment. Mixing controls the cells’access to dissolved nutrients and oxygen and also plays a key role in controlling the culture temperature. Mixing equipment has a significant impact on mixing efficiency, directly affecting power requirements and operating costs. The development of fluid dynamics in the culture medium and other fluids drives aeration processes such as bubble collapse, gas entrapment, and uniform bubble dispersion. Therefore, mixing can determine the success of a bioprocess.
Bioreactor Geometry: Most large stainless steel (or reusable) bioreactors are cylindrical with a tank height to diameter ratio (H/T) >1 . Baffles (cylindrical metal strips) are mounted on the bioreactor walls to reduce eddies and swirls in the liquid. Mixing is achieved by impellers mounted on a central agitator shaft driven by a motor. The rotating impellers pump and force the liquid to disperse within the reactor, creating a regular flow pattern that circulates through the vessel and periodically returns to the impeller area. For aeration, gas (usually air and/or oxygen) is introduced into the vessel through a sparger located below the impeller. For cylindrical bioreactors, the headspace is typically 20-30% of the total vessel volume.
The shape of the stirred tank bottom affects mixing efficiency. Most stirred bioreactors have rounded bottoms rather than flat ones to avoid sharp corners and depressions into which fluid flow can enter, thus preventing the formation of stagnant zones. The energy required to keep solids (such as cells) suspended in a stirred tank also depends on the shape of the vessel bottom. For effective mixing with a single impeller, the impeller diameter ( Di ) should be between 0.25 and 0.50 of the tank diameter ( T ) and the liquid height ( HL ) should be between 1.0 and 1.25 of T. This is because mixing intensity decreases rapidly as fluid leaves the impeller area, so large volumes of liquid in the upper part of the vessel (away from the impeller) are difficult to mix - so this should be avoided. Another aspect of vessel geometry that affects mixing efficiency is the gap ( C ) between the impeller and the tank bottom, which affects solid suspension, gas dispersion, and hydrodynamic stability. For most stirred tank bioreactor systems, the gap to fluid height ratio ( C/HL ) is typically in the range of 0.33–0.66.
Impellor type is critical to bioreactor design. The impeller system must be able to deliver enough power to the cell culture medium to achieve good mixing efficiency, uniformity, and adequate mass transfer to meet the oxygen demands of the cells. Figure 3 shows the two most common impeller designs used in reusable and single-use bioreactors: the Rushton impeller and the pitched-blade impeller. As the impeller blades rotate, they push against the adjacent fluid. This action creates areas of high pressure at the front surface and areas of low pressure behind the blades. These areas are responsible for fluid movement within the bioreactor and, ultimately, for fluid mixing. Fluid away from the impeller generally maintains a constant pressure.
Pitch blades and Rushton impellers are commonly used in bioreactors.
Fluid velocity is highest at the tip of the blade and decreases rapidly away from the impeller. As the impeller rotates, it creates rotational velocity in the surrounding fluid, which can be observed as a high velocity region next to the impeller. The Rushton impeller blade also induces radial outward flow in the vicinity. It draws fluid from the top and bottom regions of the bioreactor, creating a circular motion within the vessel. This motion enhances fluid mixing. In contrast, pitched-blade impellers create primarily axial flow.
The preferred impeller design for cell culture bioreactors is to use pitched blades (with an optimal blade diameter and stirring speed) because the blades are prone to shear damage. Pitched-blade impellers create primarily axial flow, but they can also balance axial and radial flow patterns if the blades are configured appropriately.
Axial flow is necessary for top-to-bottom mixing in stirred tank bioreactors, and pitched-blade impellers (where the blades are at an angle of less than 90° to the plane of rotation) can effectively create this flow. fluid exiting the impeller is driven downward until it is deflected from the bottom of the vessel. The fluid then spreads and flows upward along the vessel wall before being pulled back toward the impeller. The swirling flow necessitates baffles to break up the vortices that form along the vessel walls.
Pitch-blade impellers, when stirred at sufficiently high speeds in low-viscosity media such as water and cell culture media, produce a turbulent region of high shear and rapid mixing near the impeller. This high shear region is responsible for bubble collapse in bioreactors using spargers. the turbulent kinetic energy is not evenly distributed throughout the tank, with the highest values mostly occurring in the region close to the impeller. The turbulent kinetic energy levels in the rest of the tank, away from the impeller, are an order of magnitude lower than the maximum values measured.
Axial flow is useful when strong vertical flow is required—for example, to suspend solids or cells in a fluid. The ability to operate pitch-blade impellers in either upflow or downflow mode is an important requirement, and bidirectional motors can provide this capability. For most animal cell culture systems, these impellers are set to the upflow pumping mode. However, the downflow option can be used to suspend adherent cell cultures on microcarriers at low speeds and low specific power input to prevent cells from falling off the carriers.
Disk-mounted impellers with six straight blades, commonly known as Rushton turbines, produce radial flow. They are frequently used in microbial fermentations because they can generate very high shear forces, thus providing efficient gas dispersion. Rushton turbines produce a high velocity liquid flow radially outward from the impeller toward the tank wall.
The fluid is split in half, with one flowing upward and the other flowing downward toward the tank bottom. The overall flow in the vessel therefore consists of two large annular vortices, one above the impeller and the other below it.
Another feature of Rushton impellers is that they produce a trailing vortex in the fluid behind the horizontal edge of each flat impeller blade. Eddies play a crucial role in determining mixing performance, since most mixing occurs in the vicinity of the vortices produced by the impeller blades. These trailing vortices also provide gas dispersion in gas distributor systems. The associated steep velocity gradients are a major source of turbulence. One reason Rushton impellers are widely used in microbial fermenters is their ability to handle high gas flow rates and provide efficient gas dispersion.
The power required to achieve a given agitator speed depends on friction and form drag (caused by the pressure difference between the front and rear of the impeller blades), which resist the impeller from rotating. Friction and form drag produce a torque on the agitator shaft. The power input can be determined experimentally by measuring the induced torque (Equation 4):
P = 2πNiM
Where P is power, Ni is the impeller speed, and M is torque.
The power required to mix liquids without gases depends on the agitator speed, impeller shape and size, tank geometry, and liquid density and viscosity. The relationship between these variables is usually expressed as a dimensionless power (Equation 5):
NP = P/ρNi3Di5
Where NP is the power number, P is the power, Ni is the impeller speed, and Di is the impeller diameter.
The power number is analogous to the drag coefficient of a stirred system. The relationship between NP and Re is usually determined experimentally for a variety of impeller and tank configurations. Once the flow becomes turbulent, the power number for different impeller designs becomes constant. Under turbulent conditions in stirred tanks, the power number for a Rushton impeller is usually constant at 5, while the power number for an axial pitched blade impeller is approximately 1. Therefore, a Rushton impeller has a strong form drag, produces high torque, and transmits more power at the same operating speed compared to a pitched blade impeller.
Fluid Flow: The rotating impeller blades pump the fluid in the bioreactor vessel. The volume flow rate of the fluid leaving the impeller is a characteristic of the impeller design and varies with operating parameters such as impeller speed and impeller size. The dimensionless flow number indicates the effectiveness of the pumping process (Equation 6):
Nflow = Q/NiDi3
where Q is the volume flow rate of the fluid leaving the impeller blades, Ni is the impeller speed, and Di is the impeller diameter.
For the same input power, a pitched-blade impeller produces almost 3 to 4 times the flow rate of a Rushton impeller. This is why the former design is considered to have high pumping capacity and mixing operation efficiency, while the latter is considered to have lower pumping efficiency.
For good mixing in a stirred vessel, the velocity of the fluid leaving the impeller must be sufficient to carry the material into the farthest areas of the vessel. The circulating fluid must also sweep through the entire vessel in a reasonable amount of time. The fluid flow must be turbulent to achieve good mixing, which can be described as a combination of three physical processes (1): distribution, dispersion, and diffusion. Distribution is also called "macromixing" and diffusion is called "micromixing". Dispersion can be classified as either macromixing or micromixing, depending on the scale of the fluid motion.
Distribution is the process by which a fluid is transported to all areas of a stirred vessel by the bulk circulation flow. It is an important process in the mixing process and is usually the slowest step because the fluid has a long distance to travel in a long circulation path. Dispersion breaks up the bulk flow into smaller and smaller eddies, which helps the material move quickly through the vessel. The degree of uniformity that can be produced by dispersion is limited by the size of the smallest eddy that can form in a particular fluid. To achieve mixing smaller than the smallest eddy, diffusion becomes an important process. This micromixing occurs relatively quickly and over shorter distances than those involved in distribution.
Mixing time (tm ) is a useful parameter for assessing the overall mixing rate in a stirred vessel. It is the time required to achieve a given degree of uniformity starting with completely separated materials. Mixing time can be measured by injecting a tracer material (usually an acid, base, or concentrated salt solution) into the vessel and tracking its concentration at a fixed point in the vessel.
When a small tracer pulse is added to a fluid in a stirred tank that already contains a certain concentration ( Ci ) of tracer material, a concentration response curve like the one in Figure 6 can be expected. Relatively high concentrations are detected each time the bulk flow carries the tracer to the measurement point before mixing is complete. The time between peaks in concentration is approximately equal to the average time required for the fluid to traverse one overall circulation loop, called the cycle time ( tc ). After several cycles, the desired uniformity will be achieved.
After the tracer dye is injected into the stirred tank, the mixing time (tm ) is determined based on the concentration (C) response; Cf = final concentration, Ci = intermediate concentration, tc = cycle time.
The mixing time is usually expressed as the time at which the tracer concentration differs from its final concentration (Cf ) by less than 5-10% of the total concentration difference (Cf -Ci ). At tm, the tracer concentration is relatively stable and the fluid composition is close to uniform. For industrial-scale bioreactors, this takes several minutes.
Liquid phase mixing is critical in large-scale bioreactors because, in most cases, feed ingredients, bases or antifoaming agents are added at the top surface of the fluid. These additions must be distributed rapidly throughout the culture to achieve uniformity without inducing local concentration gradients. The homogenization process is governed by the dominant flow pattern and information about the overall mixing conditions in the bioreactor can be obtained from the tm measurement.
A study on large-scale bioreactor
rs using the iodine decolorization technique was reported by Sieblist et al. The data in Figure 7 show that the spatial decolorization patterns and decolorization speeds of the different impeller types vary greatly at the same power input, using three Rushton impellers and three pitched-blade impellers. These results provide experimental evidence that impellers that induce axial flow can reduce tm by about a factor of two. The reason is that the pitched-blade impellers pumping axially downward induce a more extensive flow structure, which significantly improves mixing from top to bottom; the Rushton impeller causes flow regionalization, resulting in a decrease in overall mixing efficiency, so the mixing time is longer.
Mixing time ( tm ) determined in a 400 L bioreactor equipped with three Rushton impellers (circles) or three pitched blade impellers (triangles); data fit the correlation reported by Ruszkowski; D = impeller diameter, H = vessel height, T = vessel diameter, ε = local turbulent energy dissipation rate per unit mass of fluid, θ95% = time required to reach 95% homogeneity in the bioreactor.
A surprising finding of this study is that mixing time depends only on the bioreactor geometry and not on the stirring system. Different impeller configurations affect the constant factor (10.5 or 17.9) in Ruszkowski's empirical correlation. Another experiment reported by Sieblist et al. showed that mixing time depends critically on experimental conditions, in particular the location of tracer addition in the bioreactor. Figure 8 shows that adding tracer close to the impellers has a much greater effect than adding it at the control point (liquid surface), which reduces mixing time. This demonstrates the importance of adding substrates and corrective agents (e.g., bases and antifoams) to the culture close to the stirring paddles so that they can be rapidly distributed throughout the culture. The implications of this have long been understood; however, it is not universal practice.

 English
English français
français Español
Español русский
русский português
português العربية
العربية





